Excursion

Memory limit: 128 MB

Byteasar is planning a bike trip around Byteland. He has selected 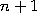towns that he is going to visit and roads that connect the pairs of consecutive towns. Each road can be described using two parameters: its length and its impression-factor, which could be either positive or negative.

The last thing that Byteasar has to do is to divide the trip into segments that will correspond to consecutive days of the excursion. Each segment must start and end in one of the selected towns and its length may not exceed 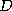kilometers. The impression-factor of a segment is defined as a square of the sum of impression-factors of the roads forming the segment. More formally, if a segment consists of roads with impression-factors 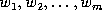, then the impression-factor of the whole segment equals .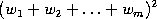

A bit surprisingly, Byteasar would like to minimize the sum of impression-factors of all the segments in his trip. Even though this idea sounds ridiculous, please help him find out how small sum can he get.

Input

The first line of input contains two integers and 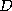(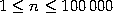, 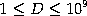) that represent the number of roads in Byteasar's trip and the upper bound for the length of a single segment of the trip. The following lines contain descriptions of the roads: the 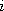-th line contains two integers 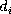and 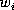, (, 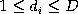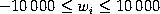) that denote the length and the impression-factor of the -th road.

Output

The only line of output should contain one integer: the minimum possible sum of impression-factors of all the segments in Byteasar's trip.

Example

For the input data:

5 15
7 4
8 -5
4 2
1 -1
2 4

the correct result is:

14

Task author: Adam Karczmarz.